REI Analysis in ancient Babylon

The basic mathematical and conceptual framework of real estate investment analysis was formed 4000 years ago in ancient Babylon.

All formulas and calculations are under the spoilers. Feel free not to open them. The point of the article is fully understood without formulas and calculations.

Difficulty: medium. 9 min read.

Math of REI analysis

Jeff Rohde wrote:

Here’s a look at the 15 most important real estate indicators for rental property investors to use in their business. The good news is that all metrics to evaluate real estate are very easy to use.

15 most important formulas of REI indicators

1. Cash Flow = Total Income – Total Expenses
2. Cash on Cash Return = Cash Received / Cash Invested
3. Gross Operating Income = (Total Potential Income – Vacancy Allowance) + Miscellaneous Income
4. Operating Expense Ratio = Operating Expenses / Gross Operating Income
5. NOI = Gross Operating Income (GOI) – Operating Expenses (excluding debt service)
6. Cap Rate = NOI / Property Cost or Value
7. Rent/Cost = Monthly Rent / Property Price
8. Operating Expenses = Monthly Rent (Operating Income) x 50%
9. Maximum Allowable Price = (After Repair Value x 70%) – Rehab Costs
10. Gross Rent Multiplier = Property Value / Annual Gross Rental Income
11. Loan to Value = Loan Amount / Property Price
12. Debt Service Coverage Ratio = Net Operating Income / Mortgage Payment
13. Vacancy Rate = Number of Days Vacant / 365 Days per Year
14. Depreciation Expense = Property Value (excluding land) / 27.5 years
15. IRR formula looks like:

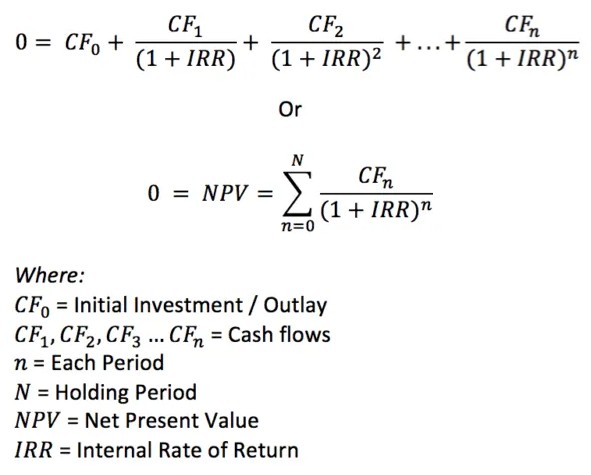
(Don't be afraid of the IRR formula. It's still calculated using four arithmetic operations. Adding is repeating the addition several tim  es. Exponentiation is multiplying a number by itself several times).

We can conclude two things after studying the most important REI indicators.

Conclusion 1. Modern formulas of classical REI analysis are based on four arithmetic operations:

• Addition
• Subtraction
• Multiplication
• Division.

Conclusion 2. REI Formulas are really extremely simple and short. In the vast majority of cases, 1-2 arithmetic operations are enough to calculate the indicator.

Babylonian Math

In the 19th century archaeologists found a library in the ruins of the ancient city of Nineveh. It was 400 well-preserved clay tablets from ancient Babylonia. The tablets were full of mathematical calculations and formulas.

The tablets were the source of our knowledge of the Babylonian civilization, which was 2,000 years B.C.

The Babylonians 4,000 years ago could perform four operations of arithmetic. They placed information on clay tablets to speed up calculations:

• Multiplication Table
• Squares of consecutive integers
• Degrees of consecutive integers
• ...

Babylonians could summarize the progressions.

An example of calculating a progression. The Babylonians used progression to obtain the square root of 2 to the nearest 6 decimal digits:

Calculation of the square root of 2

The diagonal displays an approximation of the square root of 2 in four sexagesimal figures, 1 24 51 10, which is good to about six decimal digits.
1 + 24/60 + 51/60² + 10/60³ = 1.41421296... (The Babylonians used hexadecimal arithmetic instead of decimal arithmetic. Therefore, each term was divided by a degree of 60).

Babylonian progressions made it possible to calculate the square root of 2 with any accuracy:

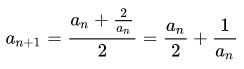
Each iteration roughly doubles the number of correct digits. Starting with 1, the results of the algorithm are as follows:

• 1
• 3 / 2 = 1.5
• 17 / 12 = 1.416...
• 577 / 408 = 1.414215...
• 665857 / 470832 = 1.4142135623746...

Babylonians also modeled exponential growth, constrained growth (via a form of sigmoid functions), and doubling time, the latter in the context of interest on loans.

Clay tablets from c. 2000 BCE include the exercise "Given an interest rate of 1/60 per month (no compounding), compute the doubling time." This yields an annual interest rate of 12/60 = 20%, and hence a doubling time of 100% growth/20% growth per year = 5 years.

The Babylonians understood the need to average data. They observed the movements of the planets, the Moon, and the Sun. The planets moved steadily. But the instruments of observation were not perfect. The measured parameters of the movement of the planets varied slightly with each observation. The Babylonians made formulas for the motion of the planets, the Moon, and the Sun. They based the formulas on average values from many years of observation.

The Babylonians considered the probability in their financial predictions. Trading houses sent ships carrying Babylonian goods to neighboring countries. When the ships returned, they brought back foreign goods. Not all ships returned due to storms, pirates,... The proportion lost depended on the route and the choice of country to trade. The proportion of irretrievable loss was known for popular routes. It was considered normal if out of 20 ships sent, one did not return. But if the route was highly profitable, a much higher percentage of lost ships was allowed.

Wikipedia has a big article on Babylonian mathematics.

Babylonian Economics 

The Babylonians used silver as money. Silver was 700 times more valuable than copper and wool. The Babylonians were well aware of inflation. During the wars with neighbors, the cost of goods would go up by as much as two times.

Individuals, temples, and trading houses were involved in financial transactions. Trading houses and temples created economic reports of their activities:

The Babylonians paid taxes, including land taxes. Wealthy people rented out buildings, housing, and animals. Babylonian trading houses engaged in banking activities. They used mortgage documents. Loan contracts were written on clay tablets.

If the borrower had a good reputation, he would return the borrowed silver at a margin of 20 to 30% per annum. Less wealthy borrowers left a mortgage in the form of a house or land. The mortgage would become the property of the trading house if the loan was not repaid on time. Over time, the trading house became the owner of dozens of buildings from debtors who could not pay back their debts. The trading house rented out these buildings. If a building gave low rent, the trading house sold it.

Babylonian REI Triangle

Babylonian advanced economy provided an understanding of the basic components of real estate investment:

• Credit
• Cumulative growth
• Mortgage
• Residential and commercial leases
• Probability of building downtime
• Inflation
• Taxes
• Averaging of historical values for forecasting
• ...

This formed the Babylonian REI Triangle 4,000 years ago:

• Motive to commit in the real estate investment - financial gain
• Means to commit in his real estate investment - advanced mathematics and the real estate rental market
• Opportunity to commit the crime - developed economy and credit

The application of mathematics to trade and financial affairs is as old as mathematics itself. History shows that as soon as a civilization develops writing, including the writing of numbers, the new technology is used in financial transactions and the appropriate mathematical ideas develop rapidly.

John H. Webb

Students in the Babylonian scribe schools studied calculus as intensely as they learned to write. The scribes who were particularly successful in calculus became civil engineers, irrigation engineers, surveyors, bookkeepers, and what are now called "analysts."

It's hard to understand, but the Babylonian indicators and formulas of real estate investment were similar to modern ones. The differences were mainly due to some difference between the Babylonian and modern economies. But the differences were not due to the flawed nature of Babylonian mathematics. A Babylonian REI analyst would have had no trouble calculating our modern REI KPI set. He would click IRR formulas like peanuts:

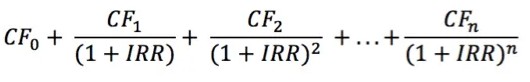
The spread of computing and trading technologies

Since ancient times, trade between nations has entailed an intense international exchange of computing and business experience.

Merchants took their goods to distant lands and brought back foreign goods to sell in their own city. The trip and return took months, even years. Caravan with camels passing through the desert:

When foreign merchants came to town, they tried to stay in the local merchants' houses. They exchanged up-to-date trade information and trade practices. 

Children of local merchants worked as servants for traveling merchants. Merchants' children ran small tasks and followed the visiting merchant around the city. As they grew up, the children had time to learn several languages and the trade customs of merchants from other countries.

When a merchant's son came of age, the merchant arranged with a reliable foreign merchant for a temporary exchange of sons. The foreign merchant would bring his son and leave him to be trained by the local merchant. In return, he would take the local merchant's son back to his country and train him in established trading practices and calculations. The merchants treated other merchants' children as if they were their own.

The training of foreign merchant traditions lasted several years. It was considered good form for a merchant's son to bring home a wife from foreign merchant's daughters after his studies. Then:

• The third generation of merchant children spoke the local and foreign language fluently from an early age
• The wives of merchants' sons communicated freely with distant merchants from their native country
• The merchants, who were related through their children, often went to visit each other. They could organize international trading houses, etc.

If a merchant had several sons, he would send them to study in different countries. This diversified trade and reduced risk in the event of a trade breakdown with any country.

Babylonian Math Today

Trade relationships have helped Babylonian mathematics and the practice of computation move through countries and millennia. Even 4,000 years later we continue to enjoy the gifts of Babylonian Mathematics.

Sample 1. Babylonian time of day:

Our Babylonian-style hour is divided into 60 minutes. The minute is also divided into 60 seconds. We're pretty good with Babylonian hour math:

Sample 2. Modern calculators and computers calculate the square root of 2 using the Babylonian method.

Sample 3. The modern Classical analysis of real estate investment was founded 4,000 years ago in Babylon. Modern and Babylonian REI analysts would have easily found a common language.